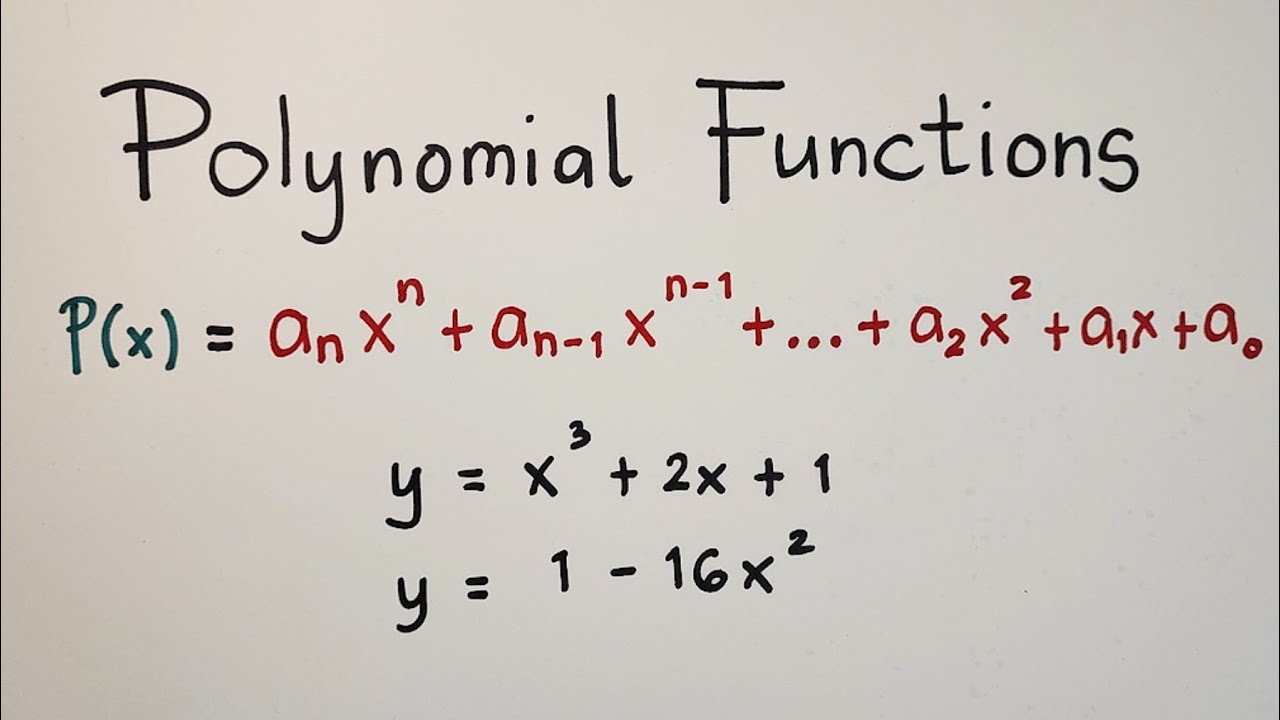Unlocking The Power Of Polynomial: Your Ultimate Guide To Understanding And Mastering

Polynomial is more than just a math term it's like the secret code that unlocks the universe's mysteries You see these babies everywhere from simple algebra to complex physics equations and even in the algorithms that power your favorite apps and games But wait what exactly is a polynomial and why should you care Well buckle up because we're diving deep into this fascinating world and trust me it's gonna be a wild ride

If you're here chances are you've stumbled across this term in your math class or maybe you're just curious about how polynomials shape our daily lives Either way you're in the right place This article will break down everything you need to know from the basics to the advanced stuff without making your brain explode

Think of polynomials as the building blocks of math They help us model real-world phenomena solve problems and even predict future trends So whether you're a student a teacher or just someone who loves math this guide will equip you with the knowledge and skills to tackle polynomials like a pro Let's get started

Read also:

Ayushi Jaiswal Rising Star In The Digital Age

What Exactly is a Polynomial?

A polynomial is like a mathematical sentence made up of variables constants and exponents strung together with addition subtraction or multiplication It's kind of like a recipe where each ingredient plays a specific role in creating the final dish The simplest form looks something like this ax^n + bx^(n-1) + cx^(n-2) + ... + k where a b c and k are constants and x is the variable

Breaking It Down

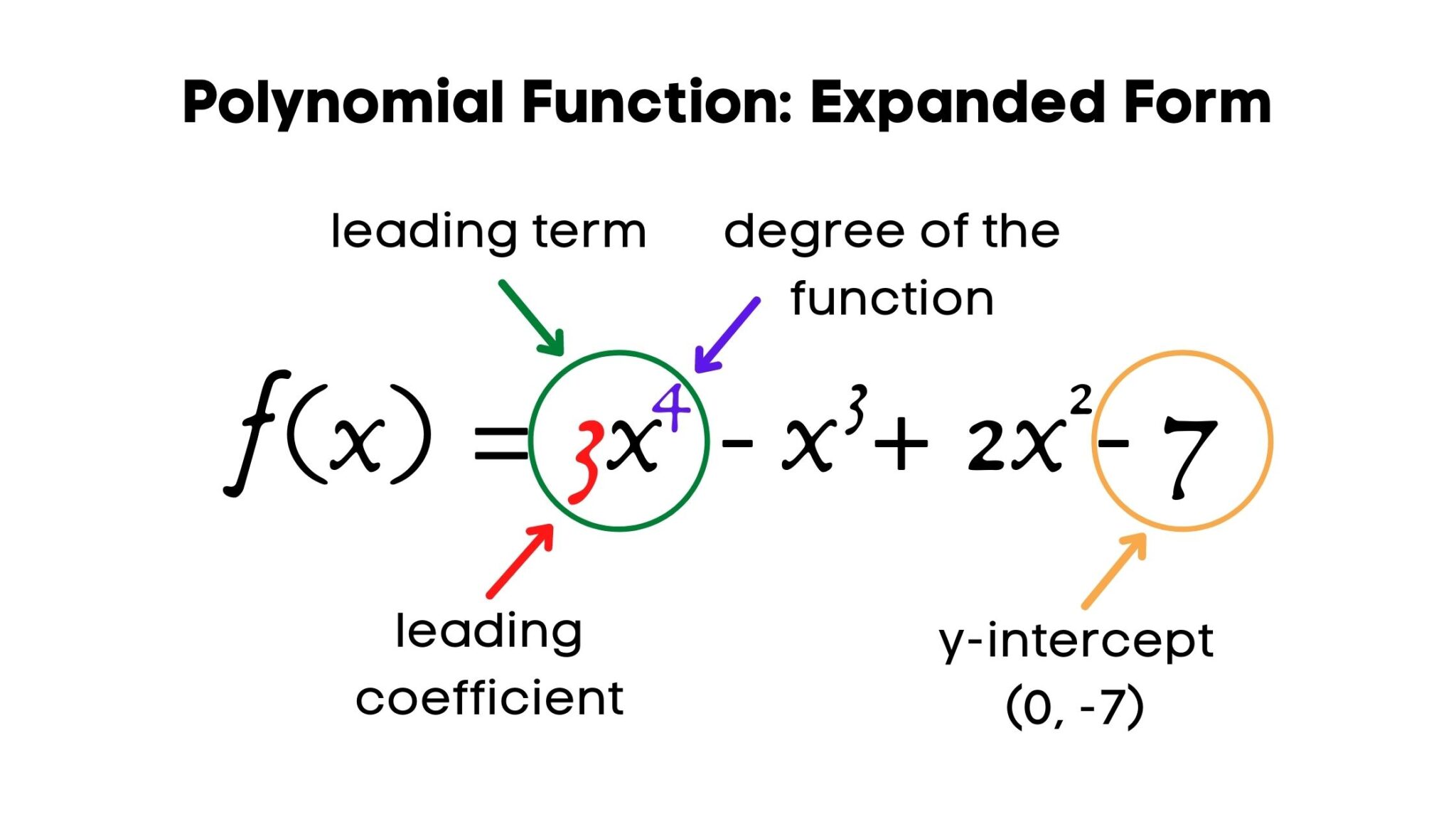
Let's break it down further A polynomial is composed of terms Each term has its own coefficient and variable raised to a non-negative integer power For example in the polynomial 3x^2 + 2x + 1 the terms are 3x^2 2x and 1 The highest power of the variable determines the degree of the polynomial which is super important because it tells us a lot about the polynomial's behavior

Why Should You Care About Polynomials?

Polynomials are everywhere They're not just some abstract concept confined to the pages of your math textbook No they're actively shaping the world around you Ever wondered how your GPS calculates the fastest route or how Netflix recommends your next binge-worthy series Polynomials are behind the scenes doing all the heavy lifting

Real-World Applications

• Engineering Polynomials are used to design bridges buildings and other structures ensuring they can withstand various forces
• Physics Polynomials help model motion energy and other physical phenomena
• Economics Polynomials assist in predicting market trends and optimizing business strategies
• Computer Science Polynomials power algorithms that make your devices smarter and faster

Types of Polynomials

Not all polynomials are created equal There are different types based on the number of terms and the degree of the polynomial Understanding these distinctions is key to mastering polynomials

Based on Number of Terms

• Monomial Single term like 5x^2
• Binomial Two terms like 3x + 2
• Trinomial Three terms like x^2 + 4x + 7

Based on Degree

• Linear Degree 1 Example 2x + 3
• Quadratic Degree 2 Example x^2 + 5x + 6
• Cubic Degree 3 Example x^3 - 2x^2 + x - 1

How to Solve Polynomial Equations

Solving polynomial equations can seem daunting at first but with the right approach it becomes a piece of cake There are several methods you can use depending on the complexity of the polynomial

Factoring

Factoring is like breaking down a polynomial into its simplest components It's especially useful for quadratic equations For example the equation x^2 - 5x + 6 can be factored into (x - 2)(x - 3)

Read also:

Shell Gas Savings How To Maximize Your Fuel Efficiency And Save Big

Using the Quadratic Formula

When factoring isn't straightforward the quadratic formula comes to the rescue It's a universal solution for any quadratic equation of the form ax^2 + bx + c = 0 The formula is x = [-b ± sqrt(b^2 - 4ac)] / 2a

Graphing Polynomials

Graphing polynomials helps visualize their behavior and understand their properties better The degree of the polynomial determines the shape of the graph For instance linear polynomials produce straight lines while quadratic polynomials create parabolas

Key Features of Polynomial Graphs

• Intercepts Where the graph crosses the x-axis and y-axis
• Turning Points The points where the graph changes direction
• End Behavior How the graph behaves as x approaches positive or negative infinity

Polynomials in Advanced Mathematics

As you progress in your math journey polynomials become even more fascinating They appear in calculus linear algebra and many other advanced fields Understanding them deeply opens doors to solving complex problems

Polynomials in Calculus

In calculus polynomials are often used to approximate functions through Taylor series This allows mathematicians and scientists to model and analyze real-world phenomena with incredible accuracy

Common Mistakes to Avoid

Even the best mathematicians make mistakes when working with polynomials Here are some common pitfalls to watch out for

Incorrect Factoring

Factoring incorrectly can lead to wrong solutions Always double-check your work and ensure each factor is accurate

Forgetting the Constant Term

The constant term might seem insignificant but it plays a crucial role in determining the polynomial's behavior Don't overlook it

Expert Tips for Mastering Polynomials

Becoming a polynomial pro requires practice and a solid understanding of the fundamentals Here are some expert tips to help you along the way

Practice Regularly

Like any skill mastering polynomials takes consistent practice Solve a variety of problems to build your confidence and improve your problem-solving skills

Use Technology Wisely

Tools like graphing calculators and software can help you visualize polynomials and check your work But don't rely on them too much Develop your intuition and understanding first

Resources for Further Learning

If you're eager to dive deeper into the world of polynomials there are plenty of resources available

Books and Online Courses

• "Algebra" by Michael Artin A comprehensive textbook covering polynomials and beyond
• Khan Academy Free online courses that break down polynomials step by step

Conclusion

Polynomials may seem intimidating at first but with the right mindset and tools they become powerful allies in your mathematical journey From basic equations to advanced applications polynomials play a vital role in shaping our understanding of the world So whether you're solving equations graphing functions or exploring advanced concepts remember that practice makes perfect

Now it's your turn Share your thoughts and questions in the comments below or check out our other articles for more math tips and tricks Together let's unlock the mysteries of mathematics one polynomial at a time

Table of Contents

• What Exactly is a Polynomial?
• Why Should You Care About Polynomials?
• Types of Polynomials
• How to Solve Polynomial Equations
• Graphing Polynomials
• Polynomials in Advanced Mathematics
• Common Mistakes to Avoid
• Expert Tips for Mastering Polynomials
• Resources for Further Learning
• Conclusion